Circuitos Eletrônicos – Atenuadores e Filtros de Áudio (parte 4)

Nos filtros abordados anteriormente, podemos notar que em ambos os casos, utilizamos o componente passivo atenuador, seja capacitor ou indutor, em série com a carga(Alto Falante).

Podemos notar também que, no caso do capacitor em série com o alto falante, construimos um filtro HPS (High Pass Filter) ou Filtro Passa Altas e no caso do indutor em sárie, construimos um filtro LPF (Low Pass Filter) ou Filtro Passa Baixas.

Desta vez, vamos construir um filtro BPS (Band Pass Filter) ou Filtro Passa Banda.

Para construir esse filtro, iremos usar os componentes dos dois filtros anteriores, ajustando seu corte de alta e de baixa nos limites desejados para a banda passante.

Agora vamos pensar um pouco... de que forma podemos limitar essa banda de frequência?

Quando inserimos o capacitor em série com o alto falante, esse capacitor se tornou um elemento de impedância variável, que em baixas frequências mantinha-se elevada, ao passo que em altas frequências diminuía, deixando a energia seguir para o alto falante.

Portanto usaremos o capacitor em série com o circuito para obter a primeira parte do filtro, que terá o seguinte efeito.

Repare que no gráfico acima, limitamos as baixas frequências e mantivemos as altas.

O cálculo da reatância capacitiva deverá acompanhar a frequência de corte, que no gráfico acima, é de 500Hz.

Continuando o pensamento anterior, nos falta agora limitar as altas frequências.

No filtro passa baixa, utilizamos o indutor em série com o alto falante para limitar as altas frequências.

O indutor, tal como o capacitor, serve como elemento de impedância váriável em acordo com a frequência. Porém, ao contrário do capacitor, o indutor mantém a menor impedância nas baixas frequências e eleva nas altas, atenuando a intensidade das altas frequências para o alto falante.

No gráfico acima, temos a atenuação das altas frequências.

Para tanto, lembremos que o cálculo da reatância indutiva desse gráfico, deve levar em conta o corte em 5KHz.

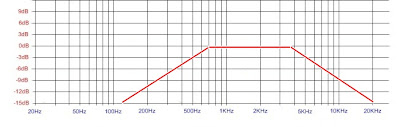
Juntando os dois filtros teremos o filtro passa banda.

O circuito seria como esse abaixo.

AMP – Amplificador de áudio

AF – Alto Falante

C – Capacitor

L – Indutor

A energia passará quando a impedância dos dois componentes(L e C) forem baixa.

Analisando o circuito, podemos notar que se trata de uma ligação em sárie entre todos os componentes. Mas o que é mais interessante, é a forma com que a ligação em série entre o indutor e o capacitor, torna possível limitar uma banda de frequência passante. A energia passa apenas quando ambos estão em sintonia.

Pois bem... e o que aconteceria se o filtro LC fosse paralelo?

No circuito acima, a energia passará de forma diferente. Teremos a somatória dos valores como dois filtros independentes.

Enquanto o indutor limita as altas frequências, o capacitor libera e enquanto o capacitor limita as baixas, o indutor libera.

Ou seja, no final das contas, somamos a banda passante de ambos os filtros.

A linha verde representa o filtro passa altas

A linha azul representa o filtro passa baixas

A linha vermelha representa a resultante do filtro.

É evidente que na configuração em paralelo o filtro tornou-se nulo, porém se mudarmos os valores dos filtros passa alta e passa baixa, podemos criar um efeito interessante. Podemos retirar uma banda indesejável.

Vamos inverter os valores de cálculo para a reatância indutiva e capacitiva.

A resultante seria, uma redução gradual de intensidade nas frequências médias chegando ao seu menor valor em 1,7Khz.

Isso pode ser interessante se desejarmos retirar excessos na resposta de um alto falante em determinadas frequências.

Circuitos Eletrônicos – Atenuadores e Filtros de Áudio (parte 3)

Como pudemos ver, o capacitor tem uma função essencial em filtros de áudio, agindo como atenuador variável conforme a freqüência aplicada.

Da mesma forma, teremos a utilização do indutor.

Assim como o capacitor, o indutor também possui a capacidade de variar a sua impedância de acordo com a freqüência aplicada.

No caso do capacitor, essa impedância é denominada de reatância capacitiva e para o indutor é denominada de reatância indutiva.

O que torna possível tal efeito é o fato de que assim como o capacitor armazena energia, o indutor também o faz, porém em um campo magnético.

A curva de carga do indutor é de características opostas, em termos de impedância, do que a curva de carga do capacitor. E é justamente essa relação que nos interessa.

 

No primeiro momento em que o indutor recebe energia, sua impedância é alta, ao passo que o capacitor começa com uma baixa impedância.

Isso se deve ao fato de que, o capacitor armazena energia em suas placas e equipara sua tensão com o circuito, quando carregado. Quando a tensão do capacitor se torna igual à tensão do circuito, a corrente se torna nula.

O indutor transforma energia elétrica em magnética, e quando seu campo satura, é visto como um curto pelo o circuito, elevando a corrente ao máximo.

Vamos ver no contexto de corrente alternada, o comportamento de um indutor em semiciclos senoidais de duas freqüências diferentes.

 

Veja que a impedância é maior para freqüências mais altas e menor para freqüências mais baixas.

Ou seja, para freqüências altas, o indutor se torna um circuito aberto, impedindo sua passagem, e para freqüências baixas, o indutor se torna um curto, deixando passar integralmente.

Esse efeito ocorre a cada semiciclo positivo e negativo, formando uma onda senoidal completa.

Calculo da reatância indutiva:

Reatância Indutiva – símbolo XL

 X_L – Reatância indutiva

f – Freqüência aplicada

L – Indutância do indutor

Vamos ver como isso funciona em um circuito real.

 

AMP – Amplificador de áudio

L – Indutor

AF – Alto Falante

No exemplo acima, temos um filtro muito comum usado para reduzir as alta freqüências para alto falantes de baixa freqüência, também conhecidos como woofer.

Esse é um filtro de primeira ordem, fornecendo portanto, uma queda de 6 dB/oitava.

Para calcular esse filtro, precisamos definir a freqüência de corte, que atenuará a intensidade de potência do woofer pela metade, ou seja -3dB.

Vamos usar 500hz como freqüência de corte.

Aproveitando o cálculo feito na primeira parte desse artigo, onde determinamos o resistor ideal para se obter uma atenuação de 3dB em um alto falante de 8 ohms, iremos substituir o resistor pelo indutor e teremos os seguintes dados:

- Indutância (L).........???

- X_L..............................3,314 Ω

- Freqüência de corte...500hz

 

Mudando a posição das variáveis na equação, temos:

 

L = 1,05mH

O valor comercial mais próximo é 1mH.

Devemos tomar o cuidado de utilizar um indutor que suporte a intensidade de corrente exigida no circuito.

Na tabela abaixo está demonstrado a atuação desse filtro simulando uma tensão de saída de um amplificador em 50Volts.

Circuitos Eletrônicos – Atenuadores e Filtros de Áudio (parte 2)

Vamos agora nos aprofundar no conhecimento sobre filtros.

Nos atenuadores, utilizamos como componente efetivo, o resistor.

Ao tratar de filtro de áudio, teremos como componentes fundamentais, o capacitor e o indutor.

Estudando primeiramente o capacitor.

Esse componente possui a capacidade de carregar energia e, portanto possui a característica de variar sua impedância em relação ao tempo.

No momento inicial de carga, o capacitor tem sua impedância igual a zero, porém com o decorrer do tempo, essa impedância se eleva ao ponto infinito, quando já está carregado.

Veja que, por este prisma, o capacitor tornou-se equivalente a um resistor que varia sua resistência com o tempo.

Ora, por quê, no gráfico, eu citei impedância ao invés de resistência?

Por concepção, a resistência transforma a energia consumida em calor. Se o caso é de carga capacitiva (sem gerar calor), denominamos reatância capacitiva. E se o caso é a junção das duas, denominamos impedância.

Perceba que, tanto a reatância como a impedância, só estarão presentes em corrente alternada ou no momento de carga do capacitor, pois em seguida se tornará um circuito aberto, sem carga alguma.

Recapitulando a característica resistiva dos componentes e suas unidades:

Resistor - Resistência

Capacitor - Reatância Capacitiva

Resistor + Capacitor - Impedância.

Voltando ao assunto da Impedância versus Tempo, verificamos que o capacitor demora um certo tempo para que o circuito chegue à impedância infinita.

Dois fatores podem mudar esse tempo:

- Variando o valor do resistor, iremos alterar o tempo de carga, produzindo maior corrente ou menor corrente de carga ao capacitor.

- Variando o valor do capacitor, teremos a mudança do tempo de carga. Se o capacitor tiver um valor de capacitância menor, ele irá carregar mais rápido do que se o valor for maior. Quanto maior a capacitância, mais energia o capacitor precisará para se carregar.

Passando essa teoria para corrente alternada, teremos mais um fator que mudará a impedância.

A freqüência irá alterar de forma direta o comportamento do circuito.

 O que seria uma curva de carga infinita, como no caso anterior(curva azul), passa a ser finita, de acordo com cada ciclo da freqüência imposta. Está valendo ciclo positivo e negativo.

Verificando que quanto maior a freqüência, menor será a impedância.

Calculo da reatância capacitiva:

Reatância Capacitiva – símbolo XC

 

 Xc – Reatância capacitiva

F – Freqüência aplicada

C – Capacitância do capacitor

Vamos ver como isso funciona em um circuito real.

 

AMP – Amplificador de áudio

C – Capacitor

AF – Alto Falante

No exemplo acima, temos um filtro muito comum usado para reduzir as baixas freqüências para alto falantes de alta freqüência, também conhecidos como tweeter.

Esse é um filtro de primeira ordem, fornecendo portanto, uma queda de 6 dB/oitava.

Para calcular esse filtro, precisamos definir a freqüência de corte, que atenuará a intensidade de potência do tweeter pela metade, ou seja -3dB.

Vamos usar 10Khz como freqüência de corte.

Aproveitando o cálculo feito na primeira parte desse artigo, onde determinamos o resistor ideal para se obter uma atenuação de 3dB em um alto falante de 8 ohms, iremos substituir o resistor pelo capacitor e teremos os seguintes dados:

- Capacitância (C).........???

- Xc..............................3,314 Ω

- Freqüência de corte...10Khz

Mudando a posição das variáveis na equação, temos:

 C = 4,8µF

O valor comercial mais próximo é 4,7µF.

Devemos tomar o cuidado de utilizar um capacitor bipolar, devido a se tratar de energia alternada.

Na tabela abaixo está demonstrado a atuação desse filtro simulando uma tensão de saída de um amplificador em 50Volts.

Circuitos Eletrônicos – Atenuadores e Filtros de Áudio (parte 1)

Para entender como funciona um filtro, precisamos primeiramente estudar um atenuador.
Assim como o filtro, o atenuador reduz a intensidade de um determinado sinal elétrico.
A diferença entre os dois, é que o atenuador reduz a intensidade do sinal, independentemente da freqüência.
Vamos começar pelo atenuador.
Em um circuito elétrico, temos sempre o gerador e a carga.
No caso abaixo, o gerador na esquerda pode ser a saída de um amplificador de som e a carga na direita, um alto falante.

Podemos atenuar a energia sobre o alto falante, adicionando um simples resistor em série no circuito.

Calculando o atenuador.
Vamos imaginar que o alto falante seja um resistor, e que possuímos uma informação muito importante, que é a impedância nominal. Dessa forma, podemos qualificar como um divisor resistivo.

Lembrando que na ligação em série entre resistores, somam-se os valores da resistência.
Impedância do alto falante – 8 ohms
Resistor atenuador – 8 ohms

Atenção: Momento polêmico!

Fica claro que a energia está dividida igualmente entre os dois resistores. Mas será que isso significa 50% de atenuação?
Calculemos pela Lei de Ohm.
Duas formulas análogas, muito importantes na eletrônica.
V = R x I
P = V x I
Onde:
V – Tensão (Volt) V
R – Resistência (Ohm) Ω
I – Corrente (Ampere) A
P – Potência (Watt) W

Vamos começar por descobrir a potência consumida pelo alto falante no momento inicial, sem o resistor atenuador.
Supondo a seguinte situação:
Saída do amplificador gerando uma tensão de 10 Volts.
Carga do alto falante com uma impedância de 8 Ohms.
Nos falta portanto, descobrir a corrente do circuito.
V = R x I
I = 10 / 8
I = 1,25 A
Calculando a potência consumida pelo alto falante.
P = V x I
P = 10 x 1,25
P = 12,5 Watts

Agora o momento importante!
Como vimos anteriormente, nossa primeira ação, seria a de adicionar um resistor de 8 ohms em série, dividindo assim em duas partes iguais a tensão do circuito.
Vejamos o que acontece.
Precisamos novamente calcular a corrente resultante (IT) da soma do resistor e do alto falante.

Resistor atenuador mais alto falante – RT = 16 Ω
V = RT x IT
IT = 10 / 16
IT = 0,625 A

A corrente total (IT) é a mesma medida em qualquer parte do circuito, por se tratar de um circuito série, mas as tensões estão divididas entre o resistor e o alto falante (RF).
Para saber qual a potência atual consumida pelo alto falante, precisamos calcular qual a queda de tensão obtida nos terminais do alto falante (VF).
VF = RF x IT
VF = 8 x 0,625
VF = 5 V

Agora sim... vamos descobrir a potência consumida pelo alto falante, tendo como atenuador um resistor de 8Ω. Vamos dar o nome de PF.
PF = VF x IT
PF = 5 x 0,625
PF = 3,125 W

Surpreso?!
Pois é... Isso se deve ao fato de que temos duas variáveis que se alteram progressivamente. A corrente e tensão.
A potência é o produto das duas.
Portanto, de que forma podemos obter uma queda de 50% na potência atenuada em relação à original?
Novamente a Lei de Ohm será a solução.
Sabemos que a potência deverá ser de 6,25 Watts e a impedância do alto falante (RF) é de 8 ohms, mas precisamos calcular a nova corrente total do circuito(IT) para obter essa Potência.
Para isso usaremos as duas fórmulas juntas.
PF = VF x IT
PF = (RF x IT) x IT
PF = RF x IT 2
6,25 = 8 x IT 2
IT 2  =  0,781
IT = 0,884 A

No circuito de ligação em série, a corrente é comum para todos os componentes.
Sabendo a nova corrente do circuito, podemos definir a resistência total do circuito. Vamos definir como RT
V = RT x IT
10 = RT x 0,884 A
RT = 10 / 0,884
RT = 11,314 Ω

Para descobrir a resistência do resistor atenuador, vamos diminuir a resistência total pela resistência do alto falante.
Resistência do atenuador - RA
RA = RT – RF
RA = 11,314 – 8
RA = 3,314 Ω

Para conferir o resultado, vamos calcular a potência do alto falante.
Corrente do circuito – 0,884 A
Impedância do alto falante – 8 Ω
Descobrindo a tensão do alto falante – VF
VF = RF x It
VF = 8 x 0,884
VF = 7,071 V

Finalmente, verificando a potência.
PF = VF x It
PF = 7,071 x 0,884
PF = 6,25 W

Aproveitando a polêmica, vamos abordar outro assunto controverso.
Antigamente era muito comum usar uma lâmpada incandescente indicada para rede elétrica de 220V em uma rede de 110V achando que a potência cairia pela metade.

No circuito abaixo, temos à esquerda o gerador, que pode ser uma tomada 110V, e na direita uma lâmpada, que pode ser aquela que você tem em casa no lustre.

Uma forma que temos para atenuar a luz da lâmpada seria simplesmente adicionar um resistor em série no circuito.

Lei de ohm novamente é a chave da questão.
Supondo as seguintes características:
Gerador – 110Volts
Lâmpada – 110Volts / 100Watts
Atenuação – 50%, portanto a lâmpada deverá trabalhar com 50Watts.
Duas formulas análogas, muito importantes na eletrônica.
V = R x I
P = V x I
Onde:
V – Tensão (Volt) V
R – Resistência (Ohm) Ω
I – Corrente (Ampere) A
P – Potência (Watt) W

Veja que uma informação muito importante nas fórmulas acima(corrente), nos falta.
A corrente, em um circuito série, é a principal informação.
Devemos encontrar, primeiramente essa informação no circuito original(sem o resistor).
Vamos chamar de I Original - IO
P = V x IO
100 = 110 x IO
IO = 100 / 110
IO = 0,909 A

Agora precisamos descobrir o valor da resistência da lâmpada, que vamos chamar de RL
V = RL x IO
110 = RL x 0,909
R = 110 / 0,909
R = 121 Ω

Definindo 50Watts para a lâmpada.
Sabemos que a potência será de 50 Watts e a resistência da lâmpada é de 121 ohms, mas precisamos calcular a nova Corrente para obter essa Potência.
Para isso, usaremos as duas fórmulas juntas.
P = V x I
P = (R x I) x I
P = RL x I2
50 = 121 x I2
I2  =  0,413
I = 0,643 A

No circuito de ligação em série, a corrente é comum para todos os componentes.
Sabendo a nova corrente do circuito, podemos definir a resistência total do circuito. Vamos definir de RT
V = RT x I
110 = RT x 0,643
RT = 110 / 0,643
RT = 171,12 Ω

Para descobrir a resistência do resistor atenuador, vamos diminuir a resistência total pela resistência da lâmpada. Resistência do atenuador - RA
RA = RT – RL
RA = 171,12 – 121
RA = 50,12 Ω

Para conferir o resultado, vamos calcular a potência da lâmpada.
Corrente do circuito – 0,643 A
Resistência da lâmpada – 121 Ω
Descobrindo a tensão da lâmpada - VL
VL = RL x I
VL = 121 x 0,643
VL = 77,782 V

Veja que para se obter 50 W a tensão deve cair para 77,78 V ao invés de 55 V antes imaginado.
Finalmente, verificando a potência.
P = VL x I
P = 77,782 x 0,643
P = 50 W

Uma observação muito importante!
Na prática, uma lâmpada incandescente altera sua resistência de acordo com o aquecimento do filamento, portanto na prática esses valores mudarão.
Se alguém fizer essa experiência, tenha em mente que a potência dissipada nesse resistor será muito alta. Aproximadamente 20 Watts.

Circuitos Eletrônicos – Filtros de Áudio Freqüência

Existem alguns tipos de filtros de áudio, dentre os quais, abordaremos os mais comuns.

 

- Filtro passa alta ou HPF(High Pass Filter), responsável por deixar passar freqüências altas e bloqueando portanto as baixas freqüências.

 

- Filtro passa baixa ou LPF(Low Pass Filter), responsável por deixar passar baixas freqüências, bloqueando as altas freqüências.

 

- Filtro passa banda ou BPF(Band Pass Filter), que deixa passar uma determinada faixa de áudio bloqueando as altas e baixas.

 

É muito comum a utilização desses filtros, seja em caixas acústicas, equalizadores, pres, microfones, etc...

A finalidade desses filtros é a de reduzir a intensidade de freqüências indesejadas. Para tanto, devemos levar em conta outro fator importante, que é a intensidade do filtro dado em dB por oitava.

A unidade “dB” é o indicativo de intensidade em que o filtro atua. A cada 3dB temos a dobra da potencia sonora. Ou seja, no caso de um filtro, 3dB, significa a metade da potencia sonora em relação à anterior. É importante entender que a relação dB é logarítma. Assim temos que, 3dB é o dobro, 6dB é o quádruplo, 9dB é o óctuplo...

Para quem quiser calcular, basta usar a seguinte fórmula.

dB = 10 log₁₀(x)

 

Onde “x” é o valor da razão de ganho que se deseja calcular. Se for o dobro, x = 2.

Oitava é o intervalo entre uma freqüência e sua dobra ou metade. A oitava superior de 100Hz é 200Hz e a inferior é 50Hz.

O momento em que se estabelece o início do corte de um filtro é quando a atenuação chega a 3dB. Desse ponto em diante, teremos a queda por oitava determinada pelo filtro. Se for um filtro de 6dB por oitava, teremos na oitava seguinte ou anterior ao corte, uma atenuação em relação ao som original de 9dB, na próxima, 15dB e assim por diante.

Uma denominação dada para filtros com relação à sua atenuação, segue a seguinte regra:

- Primeira ordem, são filtros com uma atenuação de 6dB por oitava.

- Segunda ordem, são filtros com uma atenuação de 12dB por oitava.

- Terceira ordem, são filtros com uma atenuação de 18dB por oitava.

E assim por diante... a cada ordem subsequente, segue um aumento de 6dB em relação à anterior.

 

Como podemos ver, o filtro de primeira ordem faz atenuações mais suaves, tornando seu corte mais natural. E o filtro de segunda ordem possui um corte mais enfático, evitando melhor o vazamento de freqüências indesejadas.

Circuitos Eletrônicos – Ligação em Paralelo

Muitas vezes ouvimos falar em ligar componentes em paralelo, mas como funciona essa ligação.

Como vimos no post anterior, às vezes precisamos fazer combinações de resistores para obter valores difíceis de encontrar no mercado.

No caso da ligação em paralelo, além do valor combinado, ainda temos a vantagem de aumentar a capacidade de dissipação de carga nos resistores. A potência dissipada será dividida entre os resistores. Se forem de mesmo valor, a potência dissipada em cada um será igual à potência total dividido pelo número de resistores. Dessa forma o calor pode ser distribuído por uma área maior, impedindo a queima do componente, do suporte, solda e placa de circuito impresso.

O calculo para a ligação em paralelo entre resistores é um pouco mais complicado que na ligação em série.

Para a ligação em paralelo de resistores, usamos o mesmo calculo da ligação em série de capacitores.

Ou seja:

Onde: RT é o valor total de resistência e  R1, R2, R3, os valores de cada resistor.

Dica: Se os valores dos resistores forem iguais, basta dividir o valor de um dos resistores pelo número de resistores, que no caso acima, seria por 3.

Supondo que cada resistor seja de 3,3 ohms, o valor final portanto, seria de 1,1 ohms.

A ordem dos resistores é indiferente ao valor final.

O mesmo aplica-se à ligação paralela entre alto-falantes.

Como no caso da ligação em série, em algumas situações, precisamos “casar” impedâncias entre alto-falante e amplificador de som.

Um caso, por exemplo, seria um amplificador que possua um limite mínimo de impedância de saída de 2 ohms e ligaríamos 4 alto-falantes com impedância de 8 ohms cada.

Existem alguns cuidados nesse tipo de ligação entre alto-falantes.

Devem ser conectados de forma que o positivo de um seja conectado no positivo do outro, caso contrário, eles trabalharão em oposição de fase.

É pouco comum, mas esse tipo de ligação pode também ser usada entre pilhas e baterias.

A vantagem é de manter a tensão e aumentar a longevidade da carga. Você pode alimentar um equipamento por mais tempo.

Nesse caso, é importante entender que a tensão permanecerá a mesma e a corrente se elevará na somatória das unidades.

Muito importante é ligar o positivo de uma pilha no positivo da outra.

Devemos ter uma certa atenção quanto ao mesmo tipo e condições das pilhas.

A configuração em paralelo também pode ser usada para lâmpadas.

Mas ao contrário da ligação em série, a tensão nominal da rede deve ser igual à tensão descrita na lâmpada.

A vantagem desse tipo de ligação para lâmpadas é de aumentar a iluminação apenas.

Deve-se ter o cuidado de estar ciente que, colocando lâmpadas em paralelo, estamos aumentando a corrente de consumo. Isso pode acarretar em um excesso de carga em conectores, chaves e fios elétricos. A carga deve ser calculada somando os valores de corrente de cada lâmpada.

Da mesma forma, essa configuração pode ser usada para ligação entre LEDs. Porém o ideal é que, cada LED tenha seu resistor limitador de corrente. Isso se deve ao fato de que cada LED tem uma pequena diferença na razão entre tensão e corrente. De forma que, um dos métodos mais comuns para se equalizar essa diferença, é a utilização de um resistor limitador de corrente em cada LED. Caso contrário, tendo a mesma tensão de alimentação, cada LED iria consumir uma corrente diferente. E isso poderia causar a queima do LED que tiver sua corrente máxima superada.

O calculo é o mesmo usado no o post onde descrevo a polarização dos LEDs. A lei de ohm.

Cada LED tem sua tensão particular de alimentação, portanto devemos estar atentos quanto a esse detalhe. Se ambos ou mais LEDs forem iguais, os resistores serão os mesmos. Porém existe a possibilidade de usarmos correntes diferentes para cada LED com a finalidade de produzir brilho de intensidade diferente entre eles.

Da mesma forma que na ligação em série, a ligação em paralelo entre capacitores é calculada de forma oposta à de resistores. Ou seja, entre capacitores, somam-se os valores quando em ligação paralela. CT = C1 + C2 + C3.

Circuitos Eletrônicos – Ligação em Série

Muitas vezes ouvimos falar em ligar componentes em série, mas como funciona essa ligação?

Quando trabalhamos em circuitos compostos por resistores, geralmente temos a dificuldade de encontrar valores específicos que nem sempre são vistos no mercado.

Os valores podem ser definidos facilmente por uma ligação em série.

Nesse tipo de ligação, o valor é muito simples de calcular.

Supondo um valor de 225 ohms para um determinado circuito.

No circuito em série de resistores, temos que, o valor total, é a soma dos valores dos resistores independente de suas posições.

Ou seja, para chegar ao valor de 225 ohms, poderemos utilizar na composição, um resistor de 220 ohms, outro de 4,7 ohms e outro de 0,33 ohms. Dessa forma chegamos ao valor bem aproximado do desejado.

220 + 4,7 + 0,33 = 225,03

A ordem dos resistores é indiferente ao valor final.

O mesmo aplica-se à ligação série entre alto-falantes.

Em alguns casos precisamos “casar” impedâncias entre alto-falante e amplificador de som.

Um caso, por exemplo, seria um amplificador que possua um limite mínimo de impedância de saída de 8 ohms e ligaríamos 4 alto-falantes com impedância de 2 ohms cada.

Existem alguns cuidados nesse tipo de ligação entre alto-falantes.

Devem ser conectados de forma que o negativo de um seja conectado no positivo do outro, caso contrário, eles trabalharão em oposição de fase.

Utilize preferencialmente alto-falantes de mesmo tipo e potência.

É muito comum também, usar esse tipo de ligação entre pilhas e baterias.

Nesse caso, é importante entender que a tensão se elevará na somatória das unidades, porém a corrente permanecerá a mesma.

Muito importante é ligar a polaridade do negativo de uma pilha no positivo da outra.

Outra questão muito importante, porém normalmente ignorada é de que as pilhas devem ser de capacidade e tempo de uso iguais, caso contrário, em um determinado momento, sobrará capacidade em uma pilha enquanto outra estará sem energia, causando a inversão dos pólos e conseqüentemente o vazamento químico da pilha.

 

A configuração em série também pode ser usada para lâmpadas.

Se por exemplo, tivermos uma rede elétrica de 220V e lâmpadas de 110V, podemos conectar duas lâmpadas em série e ligar normalmente na rede.

Muito importante! A potência das lâmpadas deve ser a mesma. Denominação descrita em Watts. Exemplo: 100 Watts.

Da mesma forma, essa configuração pode ser usada para ligação entre LEDs.

É o caso quando queremos aproveitar ao máximo a luz em função do consumo. Como na leitura anterior, verificamos uma grande perda no resistor que polariza o LED, agora podemos minimizar essa perda agregando outro(s) LED(s) em série.

Lembrando que a queda de tensão em um LED convencional vermelho é em torno de 2 volts, quando colocamos outro em série, essa tensão sobe para 4 volts, transformando o que seria perda sobre o resistor em aproveitamento luminoso.

No post anterior, tínhamos uma bateria de 9 volts alimentando o circuito, no qual desperdiçava 7 volts multiplicados pela corrente, em calor. Se utilizarmos dois LEDs em série, como mostra na figura acima, esse desperdício será reduzido para 5 volts multiplicado pela corrente, resultando em mais luz com a mesma energia.

Uma observação importante é que devemos ligar sempre o catodo de um LED no Anodo do outro.

Temos um caso onde ligação em série se difere quanto ao valor final da associação.

Quando ligamos capacitores em série, ele se comporta de uma forma diferenciada quanto ao visto até o momento.

Nesse caso, calculamos a capacitância somando o inverso de cada valor, e por último, invertemos o resultado da soma.

Parece complicado, mas vejamos de uma forma simplista. Se todos os valores forem, por exemplo 10µF, podemos simplesmente dividir esse valor pela quantidade de capacitores em série, que no caso é 3. Portanto o valor final será, 3,33µF.